The hybrid numbers of microwave ovens
Table of Contents
Have you ever noticed that digital microwave ovens use a kind of hybrid counting system? For example:
- You can represent forty seconds as
:40. - You can represent eighty seconds as
:80, but also as1:20. (This shows that representations are not unique). 1:00(one minute) is six times longer than0:10, which is ten times longer than0:01. (Strangely, shifting a digit sometimes divides by ten, and sometimes divides by 6!)1:80is an unusual but legal way of writing two minutes and twenty seconds. (You can try this with your own microwave!)
In this essay, I'll discuss how microwave time works, and show that another counting system — binary coded decimal (BCD) — belongs to the same family, but has markedly different properties.
1 Interpreting microwave time
Let's consider a situation where you read a time off the microwave (a
representation) and you want to know what duration of time
(magnitude) it represents. In this setup, both "magnitudes" and
"representations" will be integers, and we'll ignore the colons that
usually appear in microwave times (so we'll write the integer 100 in
place of 1:00.)
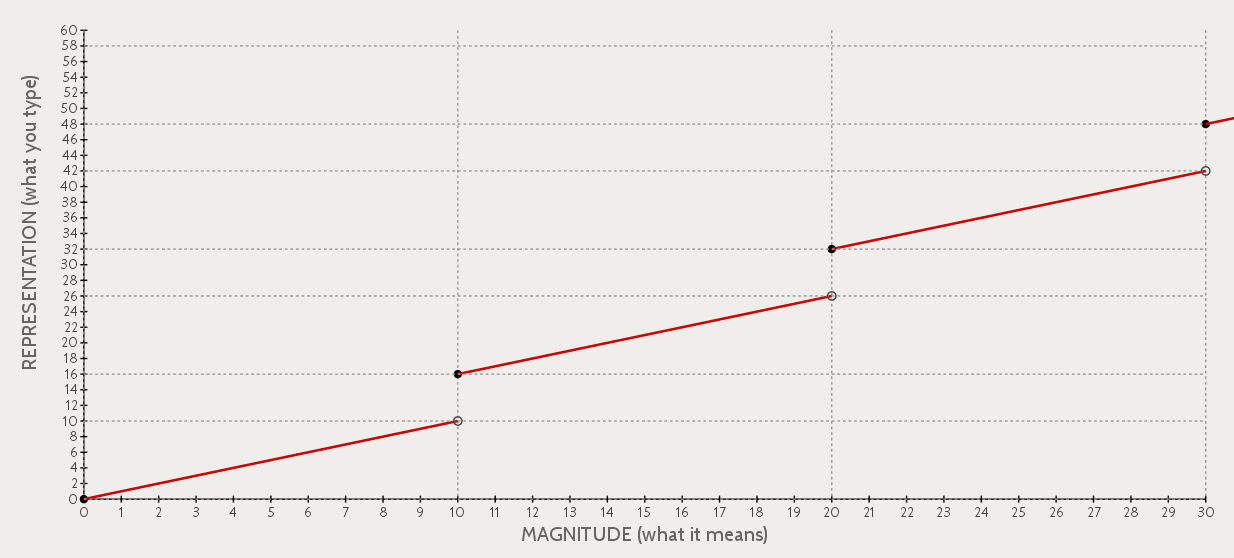
Here is a graph showing how the number you type (REPRESENTATION) in relates to the amount of time the microwave will run (MAGNITUDE). (For simplicity, the graph is drawn as a sequence of continuous lines, even though the function is only defined for integer values.)
Note that this graph shows a genuine function: each representation has exactly one interpretation. Furthermore, the microwave time representational scheme is complete in the sense that every duration can be represented in microwave time. But the representational scheme is not unique because some durations can be specified in more than one way. (In jargon, the function for interpreting microwave time is surjective but not injective).
2 Stairsteps and sawtooths
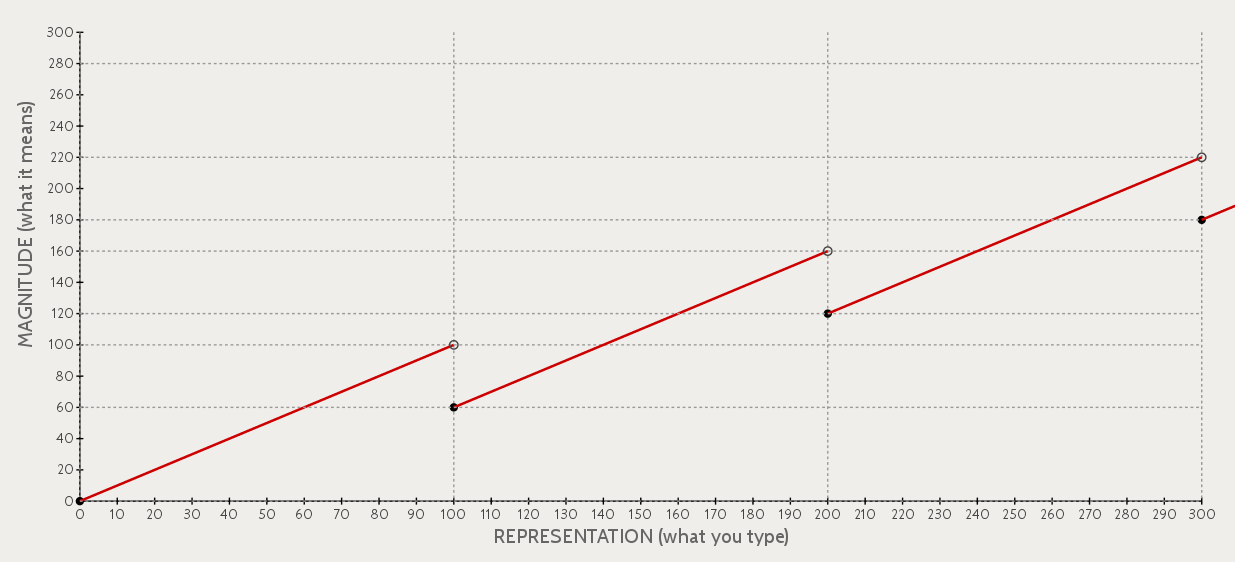
What kind of function is this? In fact, you can write it as the sum of a stairstep function and a sawtooth function. The two functions look like this:
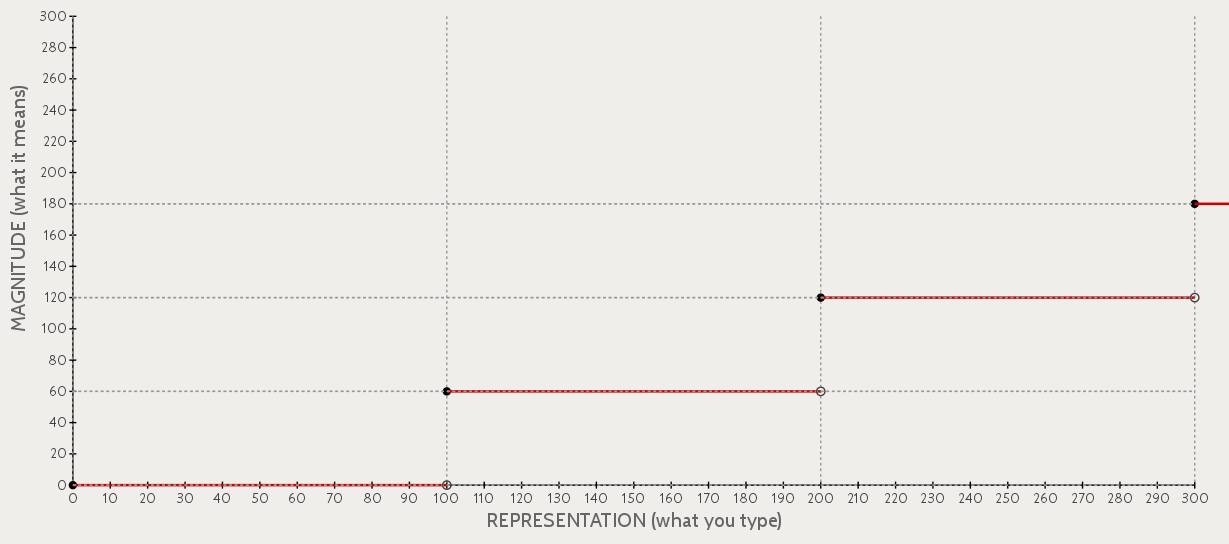
Both functions have the same "frequency", where the sawtooth repeats and the stairstep takes another step every 100 units. The unusual representational behavior comes from the height difference between the stairstep and the sawtooth.
For microwave time, the stairstep has height 60 and the sawtooth has height 100. You can imagine that by varying the heights of these functions, you can invent new microwave-like number systems with different properties. The general rule is as follows:
- If the stairstep height is less than or equal to the sawtooth height, the function will be complete (surjective), so that every magnitude can be represented in the number system.
- If the stairstep height is greater than or equal to the sawtooth height, the function will be invertible (injective), so that no magnitude has more than one representation.
- If the two heights are equal, the function is bijective; in fact, it's a straight line.
3 Binary coded decimal (BCD)
Although less familiar than microwave time, the binary coded decimal (BCD) system is another example of a stairstep-plus-sawtooth numbering system. In this section you'll see that, unlike the microwave time system, the BCD the stairstep height is larger than the sawtooth height; this means that the numbering system is invertible but incomplete.
Binary coded decimal is a way of representing integers. It's based on
the fact that any base 10 digit can be represented in binary using
four bits: 0 is 0000, 1 is 0001, 2 is 0010, …, and 10 is
1010.
To represent an integer in BCD, you consider its representation in base 10. Then you replace each digit with its four-bit binary representation and concatenate the results together. For example, to represent 413 in BCD, you would:
- Compute the digits 4 1 3.
- Replace each digit with its binary representation: 0100 0001 0011
- Concatenate the results to form one large number: 010000010011.
—
An interesting consequence of binary coded decimal is that many perfectly reasonable strings in binary are nonsense in BCD. Here are some examples:
- 10001000 (This is reasonable in binary and in BCD. In BCD, it
represents 88 (
10001000). In binary, it represents 136.) - 10101 (This is nonsense in BCD since the number of bits is not a multiple of four.)
- 1100 (This is nonsense in BCD; in binary, it would be 12 — which isn't a valid base-10 digit.)
Here's what the encoding function looks like in BCD. We take an
integer magnitude and convert it into BCD, then interpret the BCD
string of bits as a binary number. (For example, we found above that
413 is represented in BCD as 010000010011; if we interpret these
bits as a binary number, we get the integer 1043. So the point
(413, 1043) appears on the graph.)