Kinsey Strings

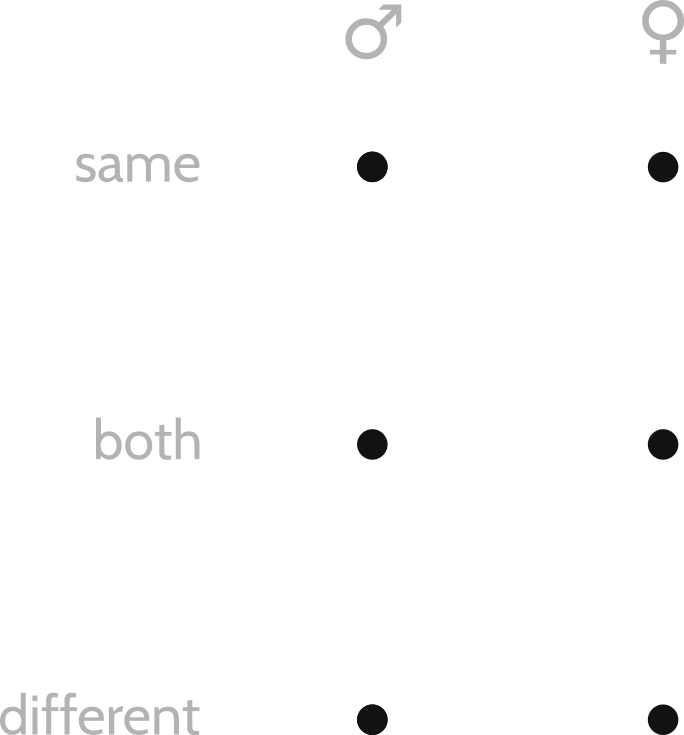
What is the shape of attraction? To find out, we can make a diagram out of string and pushpins. Suppose—reductively, but for simplicity—that there are two genders and three types of attraction: same-gendered, both-gendered, and different-gendered. Altogether, we have six different pushpins corresponding to these six different identities:

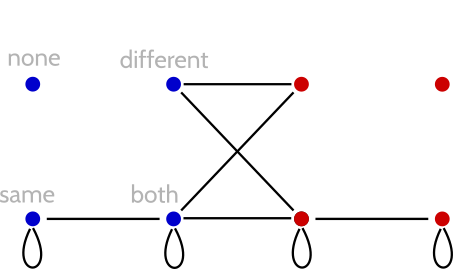
We can start by drawing arrows of attraction from each identity to the identities it's potentially attracted to. You can try this exercise yourself. When I do it, I get the following diagram:

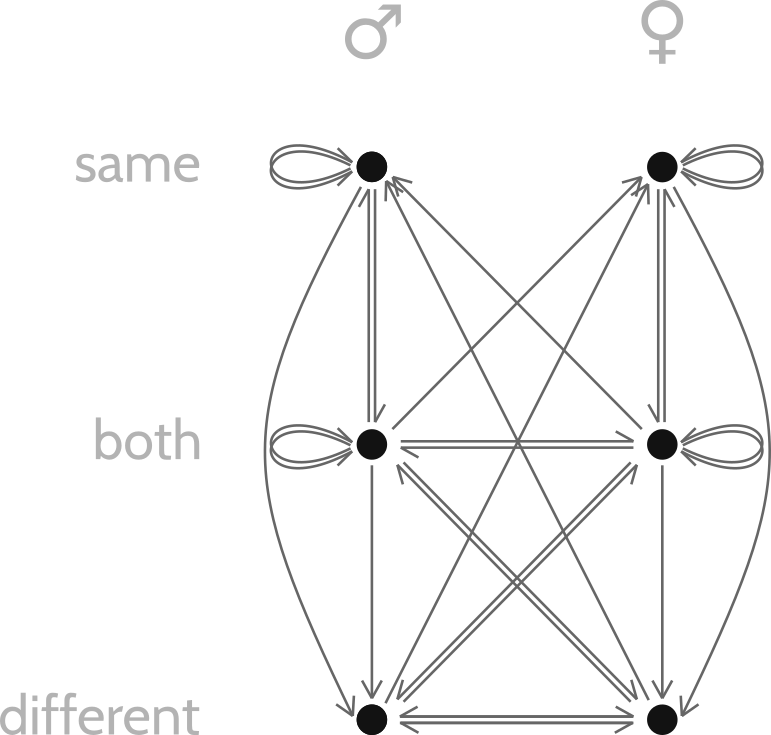
Of course, some of these attractions are unrequited—there's an arrow going one way but not the other. If we get rid of those unrequited attractions, the resulting diagram depicts the shape of mutual attraction:

Beautiful, isn't it?

Such a diagram also makes it clear how many degrees of separation there are between different identities—can you see which identities are separated by the longest path? Hint: There are three identity pairs that are maximally separated. You'd have to form a long chain of relationships to get people with those identity pairs into a relationship-by-transitivity with each other.

Also—take heart: No matter what your identity is, two out of three identities you're attracted to are attracted to you in return.

---

You can extend this approach to multiple discrete genders: \(G\) is your set of available genders and 2^G—the set of all combinations of genders—is your available orientations. When \(G=3\), there are 8 possible orientations, making 24 total identities. The mutually compatible relationship graph (like the one drawn above) looks like this:

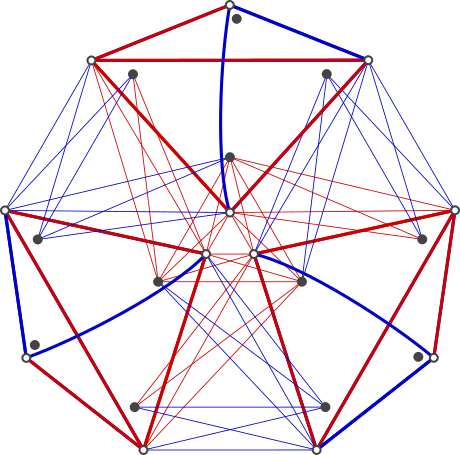
This is a graph of mutual attraction between three genders. Each dot represents an identity (gender + orientation combo). Edges represent mutual compatibility. The three genders are symmetrically arranged in three kite-shaped regions containing the eight possible orientations. Orientations consist of attraction to some combination of your own gender, the gender clockwise from you, and the gender counterclockwise from you (imagine the genders have some rock-paper-scissors clockwise order.)

If you like, you can figure out which orientation is which by looking at their connections. Otherwise, here's the complete description. Taking the topmost kite as an example, the orientations—from top to bottom and left to right—are: (1) self-only (white dot at top); (2) no attraction (disconnected black dot); (3) self-or-widders (leftmost white dot); (4) self-or-sunward (rightmost white dot); (5) widders-only (leftmost black dot); (6) sunward-only (rightmost black dot); (7) widders-or-sunward (middle black dot); (8) widders-sunward-self (white dot at bottom).

Instead of drawing a loopy edge for own-gender orientations, I use white dots. Edge color and thickness helps you read the graph, but don't otherwise mean anything.

Some interesting observations:

1. The orientations within each gender form a cube, with each axis direction representing another gender and each face being totally connected with the face of the neighboring cube on that side—you might be able to see it here by imagining that the white dots are raised out of the plane.
2. When you try to connect two separate non-ace identities through a chain of mutual compatibility links, then no matter how many genders there are, you need at most four identities total: e.g. the starting identity, a pan person whom the starting identity likes, a pan person whom the ending identity likes, and the ending identity. (So the graph diameter of the connected part is always 3, regardless of the number of genders.)
3. With the \(G=2\) picture, we didn't include ace identities (identities with no links in the graph). Now that this \(G=3\) picture includes them, we see more reasonably that half the identities you're attracted to are attracted to you in return (regardless of \(G\)).

4. The two-gender compatible relationship graph is, as you'd expect, contained in the three-gender compatible relationship graph: