, this is the result:
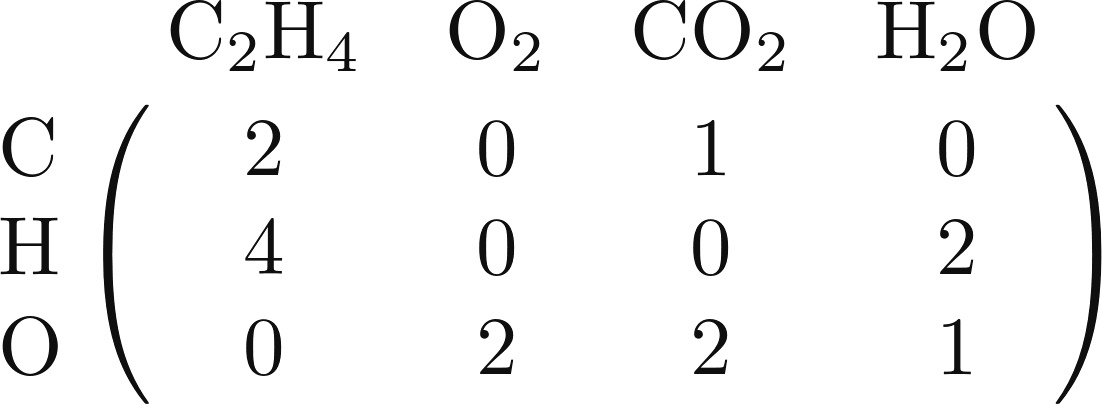
In this paper on arxiv.org, Lawrence Thorne introduces the nullspace method for balancing chemical equations. It is an improvement upon the method of solving by inspection (which results in trial-and-error and becomes unwieldy for large equations) and the method of matrix inverses (which is only applicable for equations that can be balanced in exactly one way.) Not only is the nullspace method more systematic and more widely applicable, it also provides detailed information about the all the possible ways of balancing the equation.
The null space method uses the language of matrices to describe the problem of balancing a chemical equation. Then, it uses linear algebra to solve the problem efficiently while providing you with insight into the nature of the solutions.
To start, you construct the chemical composition
matrix for the substances you are combining. This
matrix tabulates what elements each of the substances in your
equation is made of. It has one column for each substance (such
as H2SO4) and one row for every atomic
element involved (such as H, S, O)— each entry records how
many atoms of a particular element are in a particular
substance. For example, when you construct the chemical
composition matrix for the combustion of ethylene
(C2H4) , this is the result:
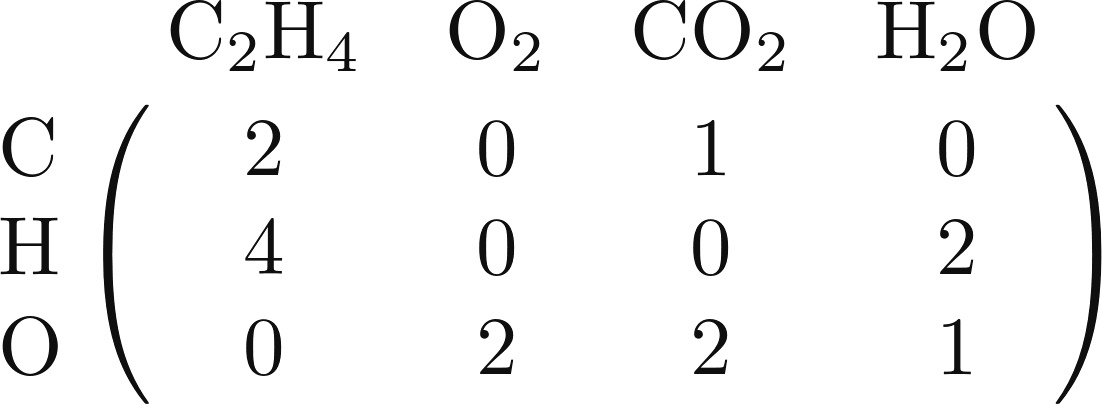
Having defined the chemical composition matrix, let's examine how we can use it. Considered as a linear transformation, the chemical composition matrix converts substance amounts into element amounts: if you specify how much of each substance you have, the chemical composition matrix converts it into a list of how much of each chemical element you have. So, referring to the combustion reaction again, if we imagine you have (for example)
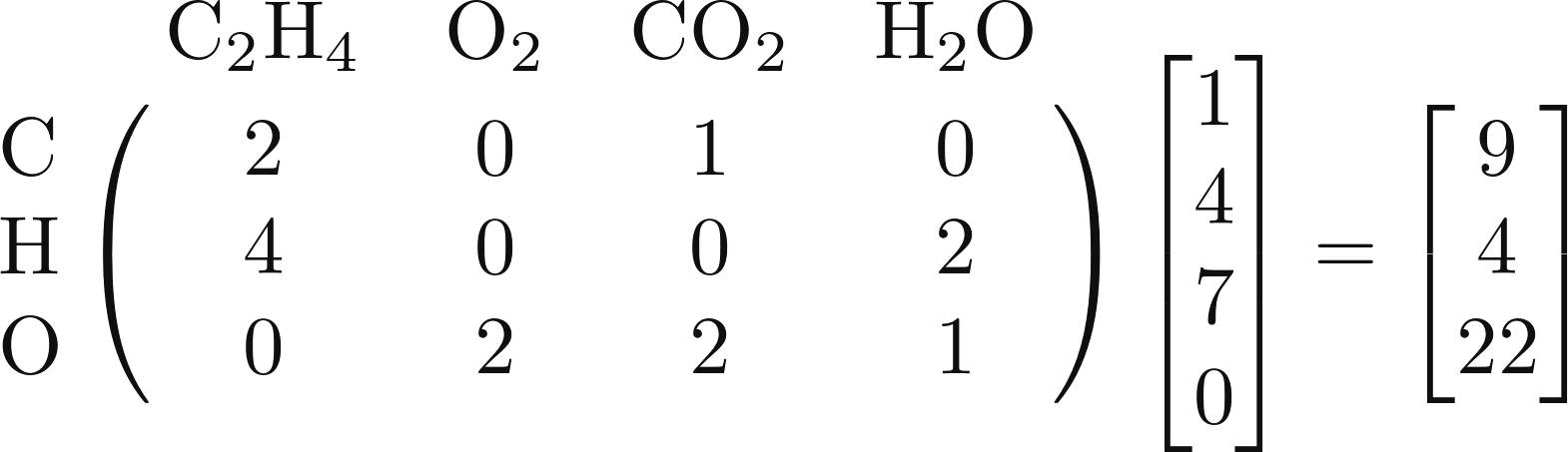In other words, in order to make 1 mole of ethylene,
4 moles of molecular oxygen, 7 moles of carbon
dioxide, and 0 moles of water, we require 9 moles of
carbon, 4 moles of hydrogen, and 22 moles of
oxygen. (Which you can confirm yourself.)
The ability to take a combination of substances and tally the amounts of each element is a key part of the balancing process. For example, suppose you have a chemical equation involving some of these substances (this equation is not properly balanced): $$10\, {\rm C_2H_4} + 3\, {\rm O}_2 \leftrightarrow 15\, {\rm CO}_2 + 4\, \rm{H_2O}$$ To find out whether the equation is balanced, you count how many of each element you have on one side and on the other side. If you have the same amount of each element on each side, the equation is balanced— otherwise, the equation is unbalanced. In this case, we have:
The chemical composition matrix offers an easier way of counting the amounts of each element on both sides of an equation. To do so, simply list the coefficients as a vector. Then, put a minus sign on all of the products' coefficients. (As far as the math is concerned, you can put minus signs either on all the reactants or on all the products. I'm just picking the products as a convention.) We can call the resulting vector the stoichiometric vector. As an example, the coefficients of our equation \(10\, {\rm C_2H_4} + 3\, {\rm O}_2 \leftrightarrow 15\, {\rm CO}_2 + 4\, \rm{H_2O}\) become the vector $$\begin{bmatrix}10 \\ 3 \\ -15 \\ -4\end{bmatrix}.$$ When we multiply our chemical composition matrix by this stoichiometric vector, we obtain the excess amount of each chemical element in our equation: $$ \begin{bmatrix} 2 & 0 & 1 & 0 \\ 4 & 0 & 0 & 2 \\ 0 & 2 & 2 & 1 \\ \end{bmatrix} \begin{bmatrix}10 \\ 3 \\ -15 \\ -4\end{bmatrix} = \begin{bmatrix}5 \\ 32 \\ -28\end{bmatrix} .$$ The vector we get as an answer says that our equation has an excess of 5 moles of carbon on the left, 32 moles of hydrogen on the left, and (as indicated by the minus sign), 28 moles of oxygen on the right.
What do you expect will happen if we instead take the coefficients from a balanced equation such as \({\rm C_2H_4} + 3{\rm O}_2 \leftrightarrow 2\, {\rm CO}_2 + 2 \rm{H_2O}\)? If we multiply the chemical composition matrix by this stoichiometric vector, we get $$ \begin{bmatrix} 2 & 0 & 1 & 0 \\ 4 & 0 & 0 & 2 \\ 0 & 2 & 2 & 1 \\ \end{bmatrix} \begin{bmatrix}1 \\ 3 \\ -2 \\ -2\end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0\end{bmatrix} .$$ This is the signature of a balanced chemical equation— the coefficients are picked in such a way that the amount of each element on the left and right side is perfectly equal. Thus, there are no excesses on either side; when we perform the matrix multiplication, we find that each entry in the resulting vector is zero.
Here are the principles we can extract from this result.
.
When balancing charges, e.g. in redox reactions, simply add a row to the chemical composition table to account for charge. (Here, charge behaves as if it were a kind of chemical element, except the amount of charge in a substance can be negative.) The null space method will balance the equation as usual, taking into account both charge and the amount of each chemical elements.
For example, let's balance the equation[1] $$ \rm H^+ + Cr_2O_7^{2-} + C_2H_5OH \leftrightarrow Cr^{3+} + CO_2 + H_2O. $$ We can write the chemical composition matrix as $$ \begin{bmatrix} 1 & 0 & 6 & 0 & 0 & 2\\ 0 & 2 & 0 & 1 & 0 & 0\\ 0 & 7 & 1 & 0 & 2 & 1\\ 0 & 0 & 2 & 0 & 1 & 0\\ +1 & -2 & 0 & +3 & 0 & 0\\ \end{bmatrix}, $$ where the last row denotes electrical charge. (There are many other ways of writing this matrix by putting the columns and rows in a different order.)
According to the nullspace method, we transpose and augment the chemical composition matrix with an identity matrix, yielding $$ \left[ \begin{array}{ccccc|cccccc} 1&0&0&0&+1&1&0&0&0&0&0\\ 0&2&7&0&-2&0&1&0&0&0&0\\ 6&0&1&2&0&0&0&1&0&0&0\\ 0&1&0&0&+3&0&0&0&1&0&0\\ 0&0&2&1&0&0&0&0&0&1&0\\ 2&0&1&0&0&0&0&0&0&0&1\\ \end{array}\right]. $$
A quick calculation reduces this to row echelon form (not shown here). In row echelon form, we notice exactly one row containing zeros: $$ \left[ \begin{array}{ccccc|cccccc} 0&0&0&0&0&1&1/8&1/16 & -1/4 & -1/8 & -11/16 \end{array}\right]. $$ This mean that the equation can be balanced, and that essentially the only way to balance it is to use the coefficients on the right. To get rid of the fractions and put the coefficients in lowest terms, we will divide all of the coefficients by the smallest coefficient (1/16), obtaining: $$ \left[ \begin{array}{ccccc|cccccc} 0&0&0&0&0&16&2&1 & -4 & -2 & -11 \end{array}\right]. $$ Hence the balancing act is complete; we can confirm by hand that all chemical elements and electric charge are balanced by these coefficients. $$ \rm 16\, H^+ + 2\, Cr_2O_7^{2-} + C_2H_5OH \leftrightarrow 4\,Cr^{3+} + 2\,CO_2 + 11\, H_2O. $$ Moreover, we know that this is essentially the only way to balance the equation.
This section is intended for mathematically-minded readers who want to see an explanation of the methods we used to find a basis for the null space of a matrix.
The nullspace of a matrix is the set of all input vectors that produce a zero vector as output. In particular, when the matrix is a chemical composition matrix, the nullspace is the set of all coefficients of properly balanced equations.
In chemical terms, a basis for the nullspace is a set of independently balanced sub-equations. Every balanced equation you can make using the substances in the chemical composition matrix can be written as a combination of those basis-equations.
The size (dimension) of the null space is called the nullity of the matrix. The nullity of a chemical composition matrix is the number of independent balanced equations it can be split into. If zero, the equation can't be balanced. If one, the equation can be balanced in exactly one way. If more than one, the equation can be balanced in infinitely many ways by combining different multiples of the basis vectors.
A matrix is invertible just when its nullity is zero. Roughly speaking, an invertible chemical composition matrix can't be balanced because "all of the atoms can be traced back to the particular substance they came from". This means that no reaction of any kind is possible.
The rank-nullity theorem says that the rank of a matrix plus the nullity of the matrix is equal to the dimension of the matrix. In chemical terms, the rank is roughly "the number of building block components." As mentioned already, the nullity is the number of independent reactions into which the reaction can be divided. The dimension of the matrix is the number of substances involved.
Expressed in terms of this representation, the vectors \(\vec{v}_1 ,\cdots, \vec{v}_p\) form a basis of the column space of \(M\), and the vectors \(\vec{v}_{p+1},\cdots, \vec{v}_{n}\) form a basis of the null space of \(M\).
To see that the \(\vec{v}_1, \cdots, \vec{v}_{p}\) form a basis for the column space of \(M\), recall that the columns of any matrix form a basis for the column space of that matrix. Next, note that column operations (used to put matrices into column echelon form) never alter the column space of a matrix. Hence, \(M\) has the same column space as its column echelon form. The columns of the echelon form are a basis for its own column space, which is the same as \(M\)'s column space, which completes the explanation.
To see that the \(\vec{v}_{p+1}, \cdots, \vec{v}_{n}\) form a basis for the null space of \(M\), note that in the augmented matrix, every column operation we perform on \(M\) will be “recorded” in the identity matrix. (This is exactly analogous to the way you can compute the inverse of a matrix by augmenting it with the identity matrix and using Gauss-Jordan elimination.) Each \(\vec{v}_i\) is a linear combination of columns of \(M\) which yields \(\vec{w}_i\). When \(\vec{w}_i\) is zero, therefore, \(\vec{v}_i\) is a member of the null space of \(M\). These vectors are independent because they started out as the identity matrix (whose columns are all independent), and column operations do not alter the column space.The fact that these vectors span the entire null space is a consequence of the rank-nullity theorem.
Thorne offers, without proof, an alternative method for computing a basis for the null space. I believe it is based on QR decomposition, although I don't entirely understand how it works.
