A sundial projection theorem
The simplest kind of sundial is a stick (gnomon) standing up perpendicularly on a plane. On the surface of a spinning planet, the stick will cast a shadow that moves as the sun passes overhead. Over the course of one day, the tip of the shadow will trace out a shape. What shape will it be?
Assuming years are much longer than days1, the shape is one of the conic sections (ellipse, parabola, or hyperbola). You can determine which one if you know three vector quantities:
- The direction \(\vec{p}\) of the planet's spin axis.
- The position \(\vec{r}\) of the sun relative to the planet.
- The orientation \(\vec{c}\) of the sundial clock—which way is the stick pointing?
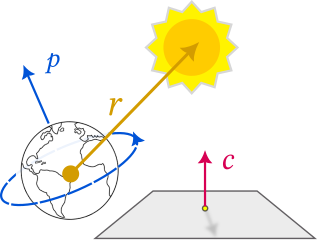
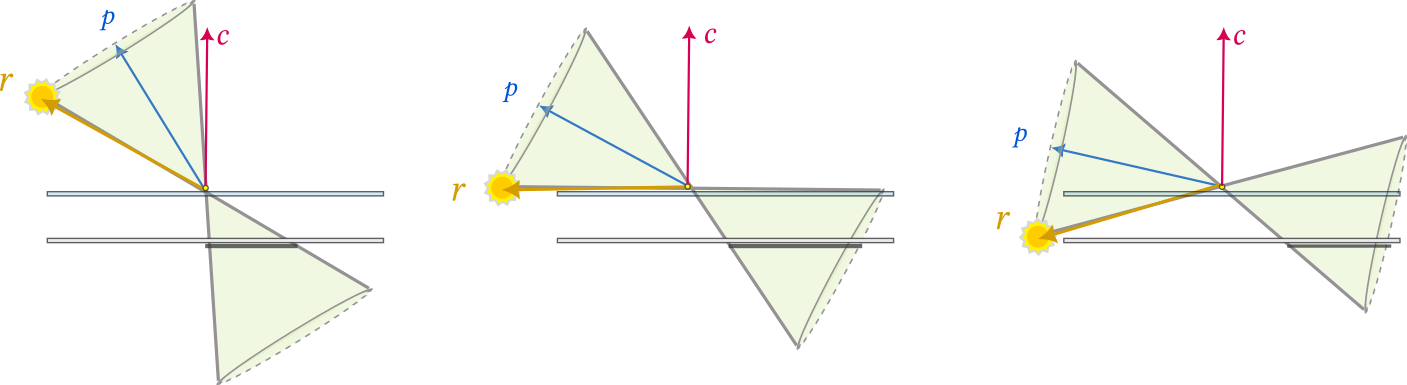
Consider the specific case of a sundial stick pointing straight up (i.e. \(\vec{c}\) points radially out from the planet's center). There is a critical plane passing through the tip of the stick and parallel to the ground (see blue plane below). Whenever the sun is above this critical plane, the stick will cast a shadow somewhere on the ground. As the sun gets closer and closer to the critical plane, the shadow will get longer and longer—like the long shadows of dusk and dawn. When the sun is level with the critical plane, the rays of light from the sun will pass parallel through the plane and never hit the ground. (When the sun is below the critical plane, the rays of light from the sun will pass up through the stick and never hit the ground either.)
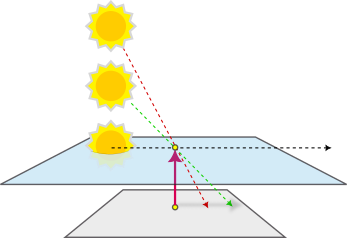
The geometry of the situation is completely determined by the number of times the sun crosses the critical plane during one daily revolution. Depending on position, it can cross zero times, one time, or two times:
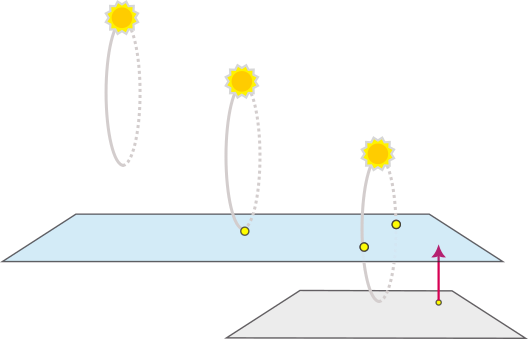
It turns out these lead to shadows with specific conic section shapes:
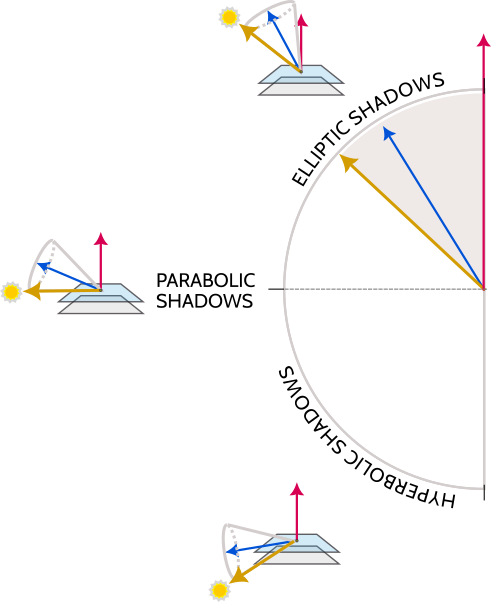
- Zero crossings (ellipse) At extreme latitudes, near the poles, we expect the sun to stay constantly above the horizon—it crosses zero times, and the daily path of the sundial shadow is an ellipse.
- One crossing (parabola) At exactly one precise latitude (which varies with the time of year), there is theoretically a point where the sun simply kisses the horizon: the sun's circular path is precisely aligned so that its lowest point touches the critical plane rather than crossing it twice, or avoiding it altogether. Sunrise and sunset become the same moment. This special case produces a shadow-path with a single-branched shape—a parabola.
- Two crossings (hyperbola) In the usual situation, we expect it to cross twice—once when rising, and again when setting. This produces a shadow path with a two-branched shape—a hyperbola.
The hyperbola, ellipse, and parabola are conic sections. Geometrically, these represent the shapes you can get by cutting a planar cross section of a cone: if the plane is roughly parallel with the base of the cone, you get elliptical cross sections. If the plane is roughly parallel to the axis of the cone, you get hyperbolic cross sections (see wikipedia image below). And if the planar slice is at one very precise angle—exactly parallel with the cone's slope—you get a parabola.
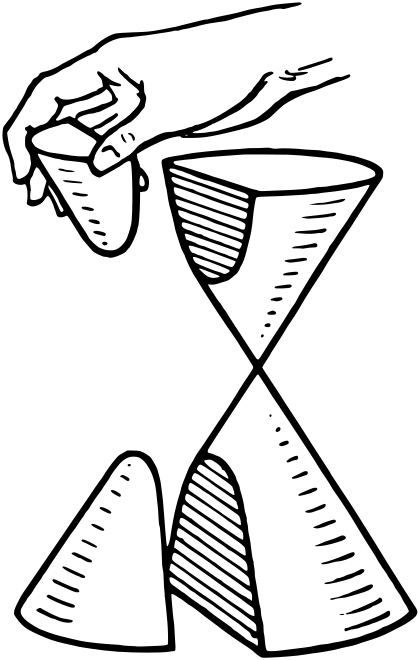
Figure 1: When a planar cut is parallel to the cone's axis, the cross section is a hyperbola.
Where are the cone and plane in this sundial situation? Here's the picture: as seen from the surface of the planet, the revolving sun traces out a daily circle in space. That circle forms the base of a cone, with the tip of the stick as its apex, and the spin axis of the planet as its central axis. The horizon—or in general, whichever angled plane that the sundial is casting a shadow on—defines the slant of the plane that cuts this cone.
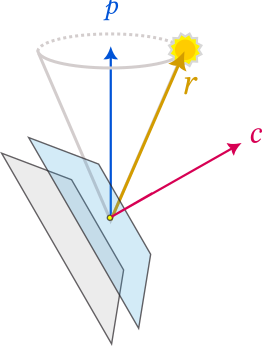
The orientation of the plane determines one parameter, the sundial clock axis \(\vec{c}\). The width of the cone is determined by the angle between the planet's spin axis \(\vec{p}\) (the axis of the cone) and the position of the sun \(\vec{r}\) (the outermost rim of the cone). This angle is constant all day as the sun moves in a circle (because the year is so long relative to the day, the planet's daily motion looks like spinning in place, so the sun's apparent motion looks like a perfect circle).
Find the angle A between the spin axis \(\vec{p}\) and the clock axis \(\vec{c}\), and the angle B between the equator and the sun's position \(\vec{r}\) (this is just the subsolar latitude, or the complement of the angle between the spin axis and the sun).
Theorem. If the sum of angles A and B is acute, then the sun lies completely above the critical plane and casts an elliptical shape. If the sum of these two angles is obtuse, then the sun crosses the critical plane twice and casts a hyperbolic shape. If the sum of these two angles is right, then the cone is lying flat on the critical plane and the sun casts a parabolic shape.
Footnotes:
unlike on planet Mercury