Manual for ANALOGY
The Golden Gallery Project
Manual for ANALOGY
Table of Contents
1 Getting started
1.1 About the program
ANALOGY is a program that models the way humans reason by analogy
when solving visual puzzles such as the following:

But the significance of ANALOGY is about more than the puzzles it
can solve. Analogies are essential to human reasoning, and especially
to the flexibility of human reasoning: whenever you can comprehend
something new by relating it to something old that you already
understand, you extend the reach of your existing knowledge for
free. If we can help computers to reason more by analogy, we can
broaden the scope of what they can do and how smart they can be. If we
can learn more about how humans reason by analogy, we may be able to
improve our ability to teach, to mediate, to explain.
1.2 How ANALOGY works
ANALOGY starts with a set of eight diagrams, and the problem "A is
to B as C is to which of the following five diagrams?".

In the first step, ANALOGY tries to find out which shapes in diagram
A correspond to which shapes in diagram B. Even though ANALOGY
assumes that only matching shapes can correspond with each other
(triangles with triangles, circles with circles, etc.), there are
often still many possible matches. Moreover, in some problems, new
shapes are added and other shapes disappear. For now, ANALOGY simply
keeps track of all possible correspondences. In the problem above, for
example, ANALOGY notices that either of the triangles in figure A
might match with the triangle in figure B.
In the second step, ANALOGY performs the same correspondence
matching between C and each of the five candidate answers. In the
problem above, for example, ANALOGY notes facts such as that the
circle in C matches the circle in 3, and that neither of the shapes in
C match the triangle in 5.
In the third step, ANALOGY analyzes the spatial relationships within
each diagram: which shapes are ABOVE, BELOW, LEFT-OF,
RIGHT-OF, INSIDE-OF, or CONTAINING which other shapes.
Fourth, ANALOGY compares the A/B correspondences with the C/i
correspondences to see how well they match. There are two parts to
evaluating how well the correspondences match:
- The first criterion is that shapes that change by appearing, disappearing, rotating, growing, shrinking, or flipping in going from A to B are matched with shapes that change in a similar way when going from C to i.
- The second criterion is that shapes have the same kinds of spatial
relationships (
ABOVE,LEFT-OF,INSIDE-OF, etc.) that their counterparts do. The more relationships they have in common, the closer the match.
For the purposes of this paper, a
correspondence-between-correspondences is what we mean by an
analogy. ANALOGY simply finds the strongest analogy (in terms of
similar transformations and similar spatial relationships), and
returns the answer diagram that goes with it.
2 Making shapes
In this section, we describe how to define shapes; you can use these methods to create your own analogy problems.
ANALOGY provides three different types of shape:
- The simplest shape is a dot — a point on the page.
- Shapes such as squares, triangles, and circles are simple closed curves. A simple closed curve is a shape made by joining pieces of lines and/or circles to form a loop. The letters D and O are simple closed curves, while the letters B and X are not.
- More complicated shapes such as the letters A and B are general connected curves. Like simple closed curves, they are made of pieces of lines and circles, but the pieces are allowed to intersect or stick out.
A diagram is a collection of these shapes arranged in a picture. Each diagram is a square of size 1, and so the shapes in each diagram will typically have coordinates between 0 and 1.
2.1 Dots
A dot is easy to define; you simply specify its position using (x,y) coordinates.
function dot(position) { var ret = { type: "DOT", position : position, draw : function($svg, attrs) { var attrs = $.extend({fill:"#000"}, attrs||{}); var xy = to_page($svg,position); $svg.circle(xy[0],xy[1], to_page($svg, 0.025 || 0.015), attrs); } }; ret.map = function(f,g) { // apply f to all the points, and g to all the curvatures. f = f || identity; var clone = $.extend(true, {}, this); clone.position = f(this.position); return clone; }; return ret; }
2.2 Simple closed curves
A simple closed curve is made of a sequence of points connected by either straight line segments, or curved pieces of circles. You specify how curved the connection between two points should be using a number called the curvature: if the curvature is 0, the connection will be a line segment. If the curvature is some other number \(k\), the connection will be a piece from a circle of radius \(1/k\).
The curvature can be positive or negative — if the curvature is positive, the connection will bend to the left as you travel from the first point to the second point. If the curvature is negative, the connection will bend to the right.
Simple closed curves are created using the function
simple_closed_curve, whose arguments are an alternating list of
location coordinates and curvatures. The last curvature in the list
connects the last point in the shape to the first point, closing the
loop.
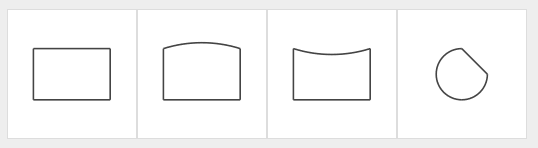
Figure 3: Four simple closed curves. The first three differ only in the curvature of one of the segments.
See in the code below how the four shapes in this image are defined. The three rectangular shapes are all identical, except for one of the curvatures. That curvature is 0 in the first picture, 1 in the second picture, and -1 in the third picture. The last picture shows how you might define a circle of radius 1/5 with a slice taken out of it.
function fig_5() { // Shows how to construct simple closed curves. var figs = [ simple_closed_curve( [0.2, 0.3], 0, [0.8, 0.3], 0, [0.8, 0.7], 0, // <<< [0.2, 0.7], 0 ), simple_closed_curve( [0.2, 0.3], 0, [0.8, 0.3], 0, [0.8, 0.7], 1, // <<< [0.2, 0.7], 0 ), simple_closed_curve( [0.2, 0.3], 0, [0.8, 0.3], 0, [0.8, 0.7], -1, // <<< [0.2, 0.7], 0 ), simple_closed_curve( [0.5, 0.7], 5, [0.5, 0.3], 5, [0.7, 0.5], 0 ) ]; // This code is used for drawing the completed figures onto the // screen. These routines will be explained later. $(figs).each(function(_, fig) { var svg = svg_new(ww,hh); document.body.appendChild(svg); var $svg = $(svg).last().svg().svg("get"); fig.draw($svg); }); }
And here is the definition of simple-closed-curve. When called, the
function returns a Javascript object with several properties and
methods.
The properties are:
- type
- which has the value "SCC" (simple closed curve), which distinguishes this shape from dots and general connected curves.
- junction
- which is the alternating list of points and curvatures that define the curve.
The methods are:
- points
- which returns a list of the shape's points, without the curvatures.
- curvatures
- which returns a list of only the shape's curvatures, without the points.
- draw
- which takes an SVG object and an optional list of pen attributes; it draws the shape onto the SVG object.
- map
- which is analogous to the
mapused for lists. Here, map takes two arguments, f and g. It applies f to every point, and g to every curvature, returning a new SCC object containing the result.mapis used for applying transformations (such as rotations) to shapes. - transform
- which takes a transformation object (defined later) and applies it to the current shape, returning a new shape.
All of the methods are functional/stateless in the sense that they do not modify the shape itself.
function simple_closed_curve() { var junction = []; for(var i=0; i<arguments.length; i++){junction.push(arguments[i])} // todo: input format checking junction.push(junction[0]); var ret = { type: "SCC", junction : junction, draw : function($svg, attrs) { var attrs = attrs || {}; for(var i=0; i<this.junction.length-1; i += 2) { draw_arc($svg, this.junction[i+0], this.junction[i+1], this.junction[i+2], attrs); } } }; ret.points = function() { var pts = []; for(var i=0; i< this.junction.length-1; i+=2){ pts.push(this.junction[i]); } return pts; }; ret.curvatures = function() { var ks = []; for(var i=1; i< this.junction.length-1; i+=2){ ks.push(this.junction[i]); } return ks; }; ret.map = function(f,g) { // apply f to all the points, and g to all the curvatures. f = f || identity; g = g || identity; var clone = $.extend(true, {}, this); for(var i in this.junction) { clone.junction[i] = (i%2==0) ? f(this.junction[i]) : g(this.junction[i]); } return clone; }; ret.transform = function (T) { // Transform the figure, keeping its center of mass fixed var T = $.extend(identity_transform, T); var center = centroid(this); return this.map( function(pt) { var qt = pt; qt = vector_subtract(qt,center); qt = vector_rotate(T.angle, qt); qt = vector_scale(T.scale, qt); qt = [(T.scale_x || 1)*qt[0], (T.scale_y || 1)*qt[1]]; qt = vector_add(qt, center); return qt; }, function(k) { return k/Math.abs(T.scale_x || T.scale)*sign(T.scale_x || 1)*sign(T.scale_y || 1); } ); }; return orient_counterclockwise(ret); }
function flip_connection(cxn) { // reverse the list and invert the curvatures var ret = cxn.slice(0).reverse(); for(var i=0; i<ret.length;i+=2) { ret[i] = ret[i] * -1; } return ret; } function revolve_curve(curve) { // Reorder the vertexes of the simple closed curve by putting the // first one at the end. This changes the representation, but not // the shape itself. var junct = curve.junction; junct = junct.slice(2,-1).concat(junct.slice(0,2)).concat([junct[2]]); return $.extend(curve,{junction: junct}); }
2.3 Connected figures
Every general connected figure has at least one junction point. A junction point is either a place where a segment terminates without connecting to anything, or a place where three or more lines meet. For example, the letter "A" has four junction points. (The corner at the top of the A is not a junction point because a line doesn't terminate there, and it isn't a place where three or more lines meet.)

In general connected figures, every junction point has a name. You define a general connected figure by specifying the locations and names of its junction points, then by describing the connections between them. Between any pair of points, there may be one connection, multiple connections, or no connection.
The simplest and most common kind of connection between a pair of junction points is a piece of a line or circle, as we saw with simple closed curves. But a pair of junction points can also be connected by a sequence of such pieces: for example, the tip of the letter A is made with two line segments strung between a pair of junction points.
As an example, here is code that defines the letter A. We start by defining the four junction points which we name A, B, C, D. (lower-left, upper-left, upper-right, lower-right).
Then we define the connections between them. Three of the connections are simple line segments. The corner of the A is made by connecting point B to the unnamed point [0.5, 0.7] via a line segment, then connecting [0.5, 0.7] to the point C via a second line segment.
var letter_A = connected_figure( {"A" : [0.3, 0.3], //V1 "B" : [0.4, 0.5], //V2 "C" : [0.6, 0.5], //V3 "D" : [0.7, 0.3], //V4 } ).add_connection( "A","B", [0], "B", "C", [0], "B", "C", [0, [0.5, 0.7], 0], "C", "D", [0] );
And here is the letter B. In this case, some pairs of junction points are connected in multiple ways.
var letter_B = connected_figure( {"A" : [0.4, 0.9], "B" : [0.4, 0.5], "C" : [0.4, 0.1]}).add_connection( "A","B",[0], "A","B",[-5], "B","C",[0], "B","C",[-5] );
Here is the definition of connected_figure which creates general
connected figures in the same way that simple-closed-curve creates
simple closed curves. In addition to the properties and methods of
simple closed curves, general connected curves also have methods
add_point and add_connection for adding labeled junction points
and for adding another connection between junction points.
The method curves takes the names of two junction points as optional
arguments. The method curves returns the list of all the connections
in the figure; if junction points are specified, it returns only the
connections starting at the first junction point and/or ending at the
second junction point. 1
function connected_figure(labels) { var ret = { type: "FIG", coordinates: labels || {}, junctions: {} }; ret.add_point = function(label, coordinates) { this.coordinates[label] = coordinates; return this; }; ret.add_connection = function() { var cxns = this.junctions || {}; var args = []; for(var i=0;i<arguments.length;i++) {args.push(arguments[i]);} for(var i=0; i<args.length-1; i+=3) { var p = args[i+0]; var q = args[i+1]; var r = args[i+2]; cxns[p] = cxns[p] || []; cxns[q] = cxns[q] || []; cxns[p].push([q,r]); cxns[q].push([p,flip_connection(r)]); } this.junctions = $.extend(this.junctions, cxns); return this; }; ret.curves = function(label_start, label_end) { // Return all the curves in the figure as alternating // coordinate/curvature lists. If labels are provided, // includes only those curves that start at the first and end // at the second. var curves = []; for(var start in this.junctions) { for(var i in this.junctions[start]) { var end = this.junctions[start][i][0]; var curve = this.junctions[start][i][1].slice(0); curve.unshift(this.coordinates[start]); curve.push(this.coordinates[end]); if((!label_start || start == label_start) && (!label_end || end == label_end)) { curves.push(curve); } } } return curves; }; ret.draw = function($svg, attrs) { var attrs = attrs || {}; var curves = this.curves(); for(var i in curves) { for(var j=0; j<curves[i].length-1; j+=2) { if(true || curves[i][j+0] < curves[i][j+2]) { draw_arc($svg, curves[i][j+0], curves[i][j+1], curves[i][j+2], attrs); } } } return this; }; ret.map = function(f,g) { // apply f to all the points, and g to all the curvatures. f = f || identity; g = g || identity; var clone = $.extend(true, {},this); for(var x in this.coordinates) { clone.coordinates[x] = f(this.coordinates[x]); } for(var start in this.junctions) { for(var i in this.junctions[start]) { for(var j in this.junctions[start][i][1]) { clone.junctions[start][i][1][j] = (j%2==1) ? f(this.junctions[start][i][1][j]) : g(this.junctions[start][i][1][j]); } } } return clone; }; ret.transform = function (T) { // Transform the figure, keeping its center of mass fixed var T = $.extend(identity_transform, T); var center = centroid(this); return this.map( function(pt) { var qt = pt; qt = vector_subtract(qt,center); qt = vector_rotate(T.angle, qt); qt = vector_scale(T.scale, qt); qt = [(T.scale_x || 1)*qt[0], (T.scale_y || 1)*qt[1]] qt = vector_add(qt, center); return qt; }, function(k) { //console.log(k/Math.abs(T.scale_x || T.scale)*sign(T.scale_x || 1)*sign(T.scale_y || 1)); return k/Math.abs(T.scale_x || T.scale)*sign(T.scale_x || 1)*sign(T.scale_y || 1); //return k/T.scale; } ); }; return ret; }
2.4 Diagrams
A diagram is a collection of shapes arranged on a single canvas. Every shape added to the diagram is given a unique automatically-generated name. Moreover, the diagram also keeps track of the spatial relationships between the shapes — which shapes are above, below, left-of, right-of, inside-of, or enclosing which other shapes.
var gensym = (function(){ var uuid = 0; return function() { uuid++; return uuid; } })(); function create_diagram() { var ret = { "type":"diagram", "figs":{}, "relations":[] }; ret.add_figure = function(fig) { var uuid = fig.type+"_"+gensym(); this.figs[uuid] = fig; // Automatically compute all relations between figures for(var u in this.figs) { if(u == uuid){continue;} var rel = spatial_relation(this.figs[uuid], this.figs[u]); if(rel[3] == 1) {this.relations.push([rel[0], uuid, u]);} else {this.relations.push([rel[0], u, uuid]);} } return this; }; ret.draw = function($svg, attrs) { var attrs = attrs || {}; for(var u in this.figs) {this.figs[u].draw($svg, attrs);} return this; }; return ret; }
3 Relationships between figures
3.1 Spatial relationships between figures
Figures are related in one of three mutually exclusive ways: they may be above/below each other, left-of/right-of each other, or within/enclosing each other.
Given two shapes, we use a crude geometric method to decide which relationship is the right one.
- First, we find the center of each shape.
- Next, we check whether it's possible that one shape is inside of the other. For simplicity, we assume it's only possible to be inside of a simple closed curve, not a dot or a general connected curve. To check whether one shape is inside another, you draw a ray originating at the center of the first shape and eminating out in any direction. Count the number of times the ray crosses the second shape: if the number is odd, the first shape is inside the second. Otherwise, it isn't.
- Assuming neither shape is inside the other, we check whether the first shape is above, below, left-of, or right-of the second shape. To do so, we divide space into four quadrants by drawing an infinite X through the center of the second shape. The top quadrant is "above", the left quadrant "left-of", and so on. We don't worry about the edge cases.
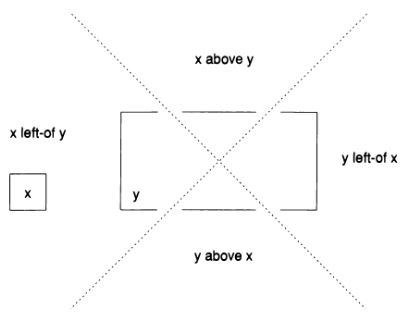
Figure 5: In the third step, above, space is divided into four quadrants.
The function spatial-relation performs this test. It returns a
triple consisting of one of the words "ABOVE", "LEFT", or "ENCLOSES",
followed by the two figures in the appropriate order.
For example, ["ABOVE", B, A] means that figure B is above figure A (or, in other words, that figure A is below figure B).
The function spatial-relation calls encloses, which performs the
enclosure test from step (2) above, and compass-relation, which
performs the position test from step (3) above.
function compass_relation(fig1, fig2) { // Returns a triple representing the relationship between figures // 1 and 2. The first entry is either ABOVE or LEFT, and the next // two entries are fig1, fig2 in the appropriate order. // Note: added fourth entry to 'triple' indicating whether fig 1 // comes first (+1) or fig2 (-1). var center1 = centroid(fig1); var center2 = centroid(fig2); var diff = vector_subtract(center2, center1); var a = diff[1] > diff[0]; var b = diff[1] > -diff[0]; if(a && b) { return ["ABOVE", fig2, fig1, -1]; } if(a && !b){ return ["LEFT", fig2, fig1, -1]; } if(!a && b) { return ["LEFT", fig1, fig2, 1]; } if(!a && !b) { return ["ABOVE", fig1, fig2, 1]; } } function encloses(closed_curve, fig) { if(!closed_curve.type || closed_curve.type != "SCC"){return false;} var center = centroid(fig); center = fig.type == "DOT" ? fig.position : fig.type == "SCC" ? fig.junction[0] : vals(fig.coordinates)[0]; var ray = create_ray(center[0], center[1], 0.777, 0.53) //Math.random()*2-1, Math.random()*2-1); var arcs = []; var n = 0; for(var i=0; i<closed_curve.junction.length-1; i+=2) { var arc = create_arc(closed_curve.junction[i+0][0], closed_curve.junction[i+0][1], closed_curve.junction[i+2][0], closed_curve.junction[i+2][1], closed_curve.junction[i+1]); var meet = figure_intersection(ray, arc); //var meet = figure_intersection_ray_arc(ray, arc, [closed_curve, fig]); if( meet == null ) { n += 0; } else if( meet.shape == "pointlist" ) { n += points(meet).length; } else if( meet.shape == "point" ) { n += 1; } //console.log("ray",ray, "arc", arc, "\nintersection",meet, n); } return n%2 != 0; } function spatial_relation(fig1, fig2) { if(encloses(fig1, fig2)) { return ["ENCLOSES", fig1, fig2, 1]; } if(encloses(fig2, fig1)) { return ["ENCLOSES", fig2, fig1, -1]; } return compass_relation(fig1, fig2); }
3.2 Reflection transformations
function translate(displacement, figure) { // Translate the figure by the given displacement vector return figure.map(function(x){ return vector_add(displacement,x); }); } function reflect(m, fig) { // Reflect the figure about the line m through the origin. var mirror_fig = fig.map(function(xy) { return vector_subtract( vector_scale( 2 * dot_product(xy, m) / dot_product(m,m), m), xy); }, function(x){return -x;}); return translate( vector_subtract( centroid(fig), centroid(mirror_fig)), mirror_fig); }
4 Aligning similar figures
The following functions compute whether two figures are similiar. If the two figures are similar, the result will be a list of potential transformations that convert one figure into the other. Each transformation can consist of a reflection, a rotation, and/or a scale factor. For our purposes, change in position (translation) is irrelevant.
The problem of aligning similar figures is tricky because it isn't clear which junctions in one figure are supposed to correspond with junctions in the other figure. We solve this alignment problem by setting it up as a constraint satisfaction problem; by using depth-first search, we look for a consistent way of pairing up the junctions from one figure and the junctions from the other.
4.1 Aligning pieces of lines and circles
The align_segment subroutine determines whether two pieces of
lines/circles are similar. The result is a single scale/rotate
transformation (no reflections at this stage), or null (if the
segments do not match).
function align_segment( start_1, end_1, start_2, end_2, curve_1, curve_2) { // Given the endpoints of two line segments, return the scale-then-rotate // transform that moves the first onto the second. // optionally take into account curvatures ("segments" which are circular arcs) var curve_1 = curve_1 || 0; var curve_2 = curve_2 || 0; var point_A = vector_subtract(start_1, end_1); var point_B = vector_subtract(start_2, end_2); var scale = distance([0,0], point_B) / distance([0,0], point_A); var a = distance([0,0], point_A); var b = distance([0,0], point_B); var c = distance(point_A, point_B); //determinant(point_A,point_B) var angle = 1*Math.acos((a*a + b*b - c*c)/(2*a*b)); angle = (angle || 0); var outer = sign(cross_product(point_A, point_B)); var inner = sign(dot_product(point_A, point_B)); if(outer <= 0) {angle = 2*Math.PI - angle;} //angle = sign(cross_product(point_A, point_B)) == -1 ? 2*Math.PI - angle : angle; if(approximately(Math.PI*2, angle)){angle = 0;} //if(curve_1 != 0 || curve_2 != 0){console.log(curve_1, curve_2, scale);} if(!approximately(curve_1/scale,curve_2)){return null;} // var flip = sign(curve_1)*sign(curve_2); // if(flip == -1){angle = (angle + Math.PI)%(Math.PI*2)} //console.log("\t\t segment", angle, sign(outer), sign(inner), start_1, end_1, start_2, end_2); // ---- NEW WAY OF CALCULATING if(true) { angle_A = Math.atan2(point_A[1], point_A[0]); angle_B = Math.atan2(point_B[1], point_B[0]); angle = angle_B - angle_A; while(angle < 0) {angle += 2*Math.PI;} while(angle >= Math.PI*2) {angle -= 2*Math.PI;} } return { scale : scale, angle: angle || 0, //sign : sign(curve_1)*sign(curve_2) }; }
4.2 Aligning simple closed curves
To align two simple closed curves:
- Standardize the points of both curves so that they are in a counterclockwise order.
- To standardize the initial points of both curves, compare the first segment of the first curve with each segment of the second curve in turn to see whether any matches.
- If there is a match, ensure that the subsequent pairs of segments also all match.
function align_simple_closed_curve(curve_1, curve_2) { // Return a list of scale-then-rotate transformations that move // curve_1 onto curve_2 (or null, if none exists.) // TODO: Compare the curvatures of aligned simple closed curves var points_1 = curve_1.points(); var points_2 = curve_2.points(); if(points_1.length != points_2.length){return null;} var curves_1 = curve_1.curvatures(); var curves_2 = curve_2.curvatures(); // Iteratively try to align the first point of curve_1 with each // point of curve_2 in turn; return a list of the transformations // corresponding to successful alignments. var transforms = []; var candidates = range(points_2.length).map(function(j){ return range(points_1.length).map(function(i) { // map segments j+i and i, generating a transform for each // (if the curvatures don't agree with the transform, return null instead) // the alignment j is valid if and only if for all i, the transforms are the same var a = align_segment( points_1[(i+0) % points_1.length], points_1[(i+1) % points_1.length], points_2[(i+j) % points_1.length], points_2[(i+j+1) % points_1.length], curves_1[i], curves_2[(i+j) % points_1.length] ); return a; // if(approximately(curves_1[i], // curves_2[(i+j) % points_1.length] / (a.scale || 1))){ // return a; // } // return null; }) }).map(function(x){ return x.reduce(function(a,b){ if(typeof b === "undefined"){return a;} if(a && b && same_transform(a,b)){return a;} return null; }); }).filter(identity); return candidates; var candidates = range(points_2.length).map(function(j){ return filter(identity, range(points_1.length).map(function(i){ var a = align_segment( points_1[(i+0) % points_1.length], points_1[(i+1) % points_1.length], points_2[(i+j) % points_1.length], points_2[(i+j+1) % points_1.length] ); if(approximately(curves_1[i], curves_2[(i+j) % points_1.length] / (a.scale || 1))){ return a; } return null; }))[0]; }); return distinct(candidates, same_transform); }
4.3 Aligning connected figures
Several subroutines are employed to align connected curves. First, you must check whether both figures have the same number of junction points (so it's possible to make a one-to-one mapping between their junction points). Then, you must see whether it's possible to match up the connections between the corresponding junctions.
Here is the method align_connected. In its search, it calls the
functions pairings and align_junction, defined below.
function align_connected(fig_1, fig_2) { if(!fig_1 || !fig_2 || fig_1.type != "FIG" || fig_2.type != "FIG" || keys(fig_1.coordinates).length != keys(fig_2.coordinates).length){return null;} // pairings? var points_1 = keys(fig_1.coordinates); var points_2 = keys(fig_2.coordinates); var pairs = pairings( points_1, points_2, function(a,b){return align_junction(fig_1, fig_2, a, b);}, false); pairs = pairs.map(function(P){ var align = zip_pairs(P.match); var transforms; for(var i in points_1) { var ts = align_junction(fig_1, fig_2, points_1[i], align[points_1[i]]); transforms = transforms ? set_intersection(transforms, ts, same_transform) : ts; } return transforms.map(function(m){m.align = align; return m;}); }).reduce(function(a,b){return a.concat(b);},[]); return pairs && pairs.length > 0 ? pairs : null; }
The subroutine pairings returns all possible pairings of two
lists. It takes an optional argument pred which determines whether
two items are allowed to be paired up, and an argument leftovers_ok
which determines whether the pairings are required to exhaust both
lists.
This generally useful method is used not only here to align two connected figures, but also later to find analogies between diagrams.
function pairings(list_1, list_2, pred, leftovers_ok) { // Return a list of all possible ways to bijectively pair up // items in list_1 with items in list_2, where each pair satisfies // pred(x,y). // By default, this function only returns pairings that exhaust // both lists. To override this behavior, set leftovers_ok to // true. var solve_constraint = function(stack, solutions) { if(stack.length == 0){return solutions;} var csp = stack.shift(); if(csp.agenda.length == 0) { if(leftovers_ok || csp.open.length == 0) { solutions.push({ match : csp.match, add : csp.open, remove : csp.remove.concat(csp.agenda), debug : csp.debug }); } } if(csp.agenda.length > 0) { var x = csp.agenda.shift(); if(leftovers_ok) { var child_csp = $.extend(true, {}, csp); child_csp.remove.push(x); child_csp.debug.push("I removed "+x); stack.push(child_csp); } for(var i in csp.open) { var y = csp.open[i]; if(pred(x,y)) { var child_csp = $.extend(true, {}, csp); child_csp.open.splice(i,1); child_csp.match.push([x,y]); child_csp.debug.push("I matched "+x+" and "+y); stack.push(child_csp); } } } return solve_constraint(stack, solutions); }; return solve_constraint([{agenda : list_1, open : list_2, remove : [], match : [], debug : [], }], []); } function pairings_optimal(list_1, list_2, pred) { // Like pairings with leftovers, but returns only those // pairings with the greatest number of matches. var pairs = pairings(list_1, list_2, pred, true); var ret = null; for(var i in pairs) { if(!ret || pairs[i].match.length > ret[0].match.length) { ret = [pairs[i]]; } else if( pairs[i].match.length == ret[0].match.length) { ret.push(pairs[i]); } } return ret || []; }
The subroutine align_endpoints takes two junctions from the first
figure and two junctions from the second figure as endpoint, and
returns the unique transformation between them (or else null).
function align_endpoints(fig_1, fig_2, start_1, end_1, start_2, end_2) { // Given two connected figures, returns the transformation that // sends label_1 ... label_2 to label_3 ... label_4, or null if // no such transformation exists. var debug = false && start_1 == "C" && start_2 == "B"; var compatible_curves = function(curve_1, curve_2) { if(curve_1.length != curve_2.length){return false;} var transform; for(var i=0; i<curve_1.length-2; i+=2) { var T = align_segment(curve_1[i+0], curve_1[i+2], curve_2[i+0], curve_2[i+2], curve_1[i+1], curve_2[i+1]); if(!T || (transform && !same_transform(T, transform, true)) ){ return null; } else { transform = T; } } return T; }; var pairs = pairings(fig_1.curves(start_1, end_1), fig_2.curves(start_2, end_2), compatible_curves, false); if(pairs.length == 0){return null;} var pairs = pairs.map(function(x){return compatible_curves(x["match"][0][0], x["match"][0][1]);}); return pairs; }
4.4 Putting it all together
The general align method can take any two figures as arguments, and
will call one of the other subroutines align_simple_closed_curve or
align_connected, as necessary. Moreover, the general align method
will also iterate over each of the three possible reflections
(horizontal, vertical, or none) while performing the comparison.
The predicate same_shape simply returns true if align returns
something other than null.
function align(fig1, fig2) { if(fig1.type != fig2.type){return null;} else if(fig1.type == "DOT"){return [{}];} else{ // TODO: ensure counterclockwise orientation of sccs var f = fig1.type == "SCC" ? align_simple_closed_curve : align_connected; var reflections = {null : identity, "vertical" : function(x){return reflect([0,1], x);}, "horizontal" : function(x){return reflect([1,0], x);} }; var ret = []; for(var r in reflections) { var x = f(fig1, reflections[r](fig2)); if(x){ret = ret.concat(x.map(function(m){ if(r != "null"){m.reflect = r;} return m;}));} } return ret.length == 0 ? null : distinct(ret,same_transform); } } function same_shape(fig1, fig2) { if(fig1.type != fig2.type){return false;} else if(fig1.type == "DOT"){return true;} else { return (align(fig1, fig2) != null); } }
5 Finding analogies
Given a list of four or more diagrams, ANALOGY produces a list of
potential analogies as follows.
- First, it finds all ways of pairing up figures in the first diagram
with figures of the same shape in the second diagram. To do so, it
calls
pairings_optimal. Because some figures may be added or deleted, theleftovers_okargument is set to true. The resulting list of possible pairings is stored in the variablepairings_1. - Next, it finds all ways of pairing up figures in the third diagram
with figures in each of the remaining diagrams. The resulting list
of possible pairings is stored in the variable
pairings_2. - Each combination of a pairing from
pairings_1and one frompairings_2is assessed for its analogical compatibility. To start with,ANALOGYrejects all pairings where a different number of figures were added or removed or kept in the first pairing compared to the second pairing. - Next, all possible ways of making a correspondence between the
added figures in each pairing, the removed figures in each
pairing, and the kept figures in each pairing are produced by
again calling the
pairings_optimalfunction. - Finally, these correspondences (which are analogies) are assessed
and sorted based on how well the analogy works. The first factor is
the number of spatial relations which each shape has in common with
its counterpart. The second factor is the similarity between the
transformations, which is measured by the
rank_transformscoring function.
function analogies(diagrams) { // Given a list of at least four diagrams, returns a list of all // possible analogies among the first three and each of the rest. // An analogy is an object containing metadata about the // correspondence between the figures. // 1. Generate the pairings with the greatest number of // matches between figures A & B, and figures C & i. // 2. Consider all pairings between AB pairings and Ci // pairings. Filter for those with the same number of matches, // adds, and removes (i.e. with the same number of shapes in each // corresponding diagram) // 3. An admissible analogy is any bijective correspondence // between added/matched/removed figures, respectively, in an AB // and a Ci pairing. var ret = []; var pairings_1 = pairings_optimal( keys(diagrams[0].figs), keys(diagrams[1].figs), function(x,y){ var transforms = align(diagrams[0].figs[x], diagrams[1].figs[y]); if(transforms && transforms.length > 0){return transforms;} return null; }); for(var i=3; i<diagrams.length; i++) { var pairings_2 = pairings_optimal( keys(diagrams[2].figs),keys(diagrams[i].figs), function(x,y){ var transforms = align(diagrams[2].figs[x], diagrams[i].figs[y]); if(transforms && transforms.length > 0){return transforms;} return null; }); //console.log(pairings_1, pairings_2); for(var ab in pairings_1) { for(var cd in pairings_2) { var pairing_ab = pairings_1[ab]; var pairing_cd = pairings_2[cd]; // If the AB and Ci pairings have a different number // of added/matched/removed figures, there can be no // analogy between them. if(pairing_ab.match.length != pairing_cd.match.length || pairing_ab.add.length != pairing_cd.add.length || pairing_ab.remove.length != pairing_cd.remove.length){ continue; } // An analog is a single pair from a pairing (along // with a keyword indicating whether it was ADDED, // REMOVED, or MATCHED. An analogy is a bijective // correspondence between analogs with the same // keyword. var convert = function(m) { var ret = []; for(var n in ["add","match","remove"]) { var mode = ["add","match","remove"][n]; ret = ret.concat(m[mode].map(function(x){ return [mode, mode == "match" ? x : mode == "remove" ? [x, null] : mode == "add" ? [null, x] : null] })); } return ret; }; var analogs_1 = convert(pairing_ab); var analogs_2 = convert(pairing_cd); var analogies = pairings(analogs_1, analogs_2, function(x,y){ return x[0] == y[0]; }, false).map(function(pairing){ return pairing.match.map( function(pair) { return pair[0][1].concat(pair[1][1]); } ); }); ret = ret.concat( analogies.map(function(a){ return {"diagram" : i, "analogy" : a, "relations_before": common_relations(diagrams[0], diagrams[2], a.map(function(y){ return [y[0], y[2]]; })).concat( a.map(function(y) { if(!y[0] || !y[2]){return false;} var ali = align(diagrams[0].figs[y[0]], diagrams[2].figs[y[2]]); //svg_diagram(0.2,diagrams[0].figs[y[0]]).appendTo($workspace); //svg_diagram(0.2,diagrams[2].figs[y[2]]).appendTo($workspace); //$workspace.append((ali && ali.length > 0) ? 'true' : 'f').append("<br/>\n"); // console.log(diagrams[0].figs[y[0]], // diagrams[2].figs[y[2]], // ali, ali && ali.length, ali && ali.length > 0); return (ali && ali.length > 0) ? ["SHAPE", y[0], y[2]] : null }).filter(identity) ), "relations_after": common_relations(diagrams[1], diagrams[i], a.map(function(y){ return [y[1], y[3]]; })).concat( a.filter(function(y) { if(!y[1] || !y[3]){return false;} var ali = align(diagrams[1].figs[y[1]], diagrams[i].figs[y[3]]); // svg_diagram(0.2,diagrams[1].figs[y[1]]).appendTo($workspace); // svg_diagram(0.2,diagrams[i].figs[y[3]]).appendTo($workspace); // $workspace.append((ali && ali.length > 0) ? 'true' : 'f').append("<br/>\n"); return ali && ali.length > 0; }).map(function(y){ return ["SHAPE", y[1], y[3]]; }) ), "convert": a.reduce(function(m,x){ m[x[1]] = x[0]; m[x[3]] = x[2]; return m; },{}), "transforms" : a.map(function(four) { var align_1 = four[0] && four[1] ? align( diagrams[0].figs[four[0]], diagrams[1].figs[four[1]]) : null; var align_2 = four[2] && four[3] ? align( diagrams[2].figs[four[2]], diagrams[i].figs[four[3]]) : null; return [set_intersection(align_1 || [], align_2 || [], same_transform), align_1, align_2]; }) } })); } } } var keyfn = function(x) { return x.relations_before.length + x.relations_after.length + x.transforms.map(function(x) { var T = x[0]; if(T.length == 0){return 0} else { return rank_transform(sort_by(rank_transform, T)[0]); } } ).reduce(function(a,b){return a+b}, 0); }; return sort_by(keyfn, ret); }
Here is the rank_transform function, which sorts transformations
based on how preferable they are. For example, here transformations
without reflections are preferred over transfromations with
reflections. (So, when a transformation could be accounted for by
either a pure rotation or a pure reflection, ANALOGY will prefer the
rotation. This is a holdover from Evans's original thesis, and
probably imitates the way people think about analogies.)
function rank_transform(T) { var scale = T.scale || 1; var angle = T.angle || 0; var reflect = T.reflect || null; if(scale == 1 && angle == 0 && !reflect) { // NO CHANGE return 0.45; } else if (angle == 0 && !reflect) { // ONLY SCALE return 0.4; } else if(scale == 1 && !reflect) { // ONLY ROTATE return 0.35; } else if(!reflect) { // ONLY SCALE AND ROTATE return 0.3; } else if(scale == 1 && angle == 0) { // ONLY REFLECT return 0.07; } else if(angle == 0) { // ONLY SCALE AND REFLECT return 0.06; } else if(scale == 1) { // ONLY ROTATE AND REFLECT return 0.05; } else { // SCALE, REFLECT, AND ROTATE return 0.03; } }
6 Appendix: Utility functions
6.1 Sequences, sets, and hash maps
The following functions provide methods for manipulating lists (arrays) in a functional (stateless) way.
function isArray(o) { return Object.prototype.toString.call(o) === '[object Array]'; } function filter(pred, coll) { var ret = []; for(var i in coll) { if(pred(coll[i])){ret.push(coll[i]);} } return ret; } function remove(pred, coll) { var ret = []; for(var i in coll) { if(!pred(coll[i])){ret.push(coll[i]);} } return ret; } function sort_by(keyfn, coll) { return coll.slice(0).sort(function(a,b){return keyfn(b) - keyfn(a);}); } function distinct(arr, is_similar) { // return a copy of the array with duplicates removed. // If is_similar is supplied, is_similar is used to judge duplicates. var is_similar = is_similar || function(x,y){return JSON.stringify(x) == JSON.stringify(y);}; return arr.slice(0).reduce(function(keep, x){ if( keep.filter(function(y){return is_similar(x,y);}).length == 0){ keep.push(x); } return keep; }, []); } function contains(coll, x){ return (coll.length != 0) && (coll[0] == x || contains(coll.slice(1), x)); } function first(coll){return coll ? coll[0] : null;} function range(n) { var ret = []; for(var i=0; i<n;i++){ret.push(i);} return ret; } function equal_arrays(arr1, arr2) { if(arr1.length != arr2.length){return false;} for(var i=0; i<arr1.length;i++) { if(arr1[i] != arr2[i]){return false;} } return true; }
Sets are essentially the same as sequences, except occasionally you
will want to form their intersection. Here, the argument is_similar
allows you to decide whether two members of the set are similar enough
that there can only be one of them in the intersection.
function set_intersection(arr1, arr2, is_similar) { var is_similar = is_similar || function(x,y){return JSON.stringify(x) == JSON.stringify(y);}; var ret = []; for(var i in arr1) { var found = false; for(var j in arr2) { found = found || is_similar(arr1[i], arr2[j]); } if(found) { ret.push(arr1[i]); } } return distinct(ret,is_similar); // return filter(identity,arr1.map(function(x) { // return arr2.reduce(function(a,b) { // return a ? a : is_similar(x,b) ? x : null; // }, null); // })); }
And with hashmaps, you can retrieve a list of keys, a list of values, or a clean copy2 of the map. The function zip-pairs will take a list of pairs and make a hash-map out of them.
function keys(m){var ret = []; for(var x in m){ret.push(x);} return ret;} function vals(m){var ret = []; for(var x in m){ret.push(m[x]);} return ret;} function clean(m) {return $.extend(true,{},m);} function zip_pairs(pairs) { return !pairs ? [] : pairs.reduce(function(m,x){m[x[0]] = x[1]; return m}, {}); }
6.2 Vectors in two dimensions
The following functions deal with vectors and square matrices of size two.
6.3 Geometric primitives
The geometric analogy program depends on an underlying system of knowledge about whether certain simple figures are intersecting, contained within each other, etc. These functions provide this underlying system.
First, to avoid making mistakes due to rounding errors, we define a function for deciding whether two numbers are approximately equal:
var iota = 0.0000001; function approximately(x,y, tolerance) { var tolerance = tolerance || iota; return Math.abs(x-y) <= tolerance;}
Because we will be dealing with plane geometric figures, we define functions for manipulating vectors and square matrices of size two:
function determinant(v,w){return v[0]*w[1]-v[1]*w[0];} function dot_product(v,w){return v[0]*w[0]+v[1]*w[1];} function cross_product(v,w) {return v[0]*w[1] - v[1]*w[0];} //signed magnitude of the cross product function midpoint(p, q) {return vector_scale(0.5, vector_add(p, q));} function perpendicular_bisector(p, q) { var m = midpoint(p,q); var d = vector_subtract(q,p); var perp = [d[1], -d[0]]; return create_ray(m[0], m[1], perp[0], perp[1]); }
function square(x) {return Math.pow(x,2);} function vector_add(v1, v2) { return [v1[0] + v2[0], v1[1] + v2[1]]; } function vector_subtract(v1, v2) { return [v1[0] - v2[0], v1[1] - v2[1]];} function vector_scale(a, v) { var w = []; for(var i in v) {w[i] = a * v[i];} return w; } function normalize(v) { var len = distance([0,0],v); if(len == 0){return v} return vector_scale(1/len, v); } function vector_rotate(angle, v) { return [v[0] * Math.cos(angle) - v[1] * Math.sin(angle), v[0] * Math.sin(angle) + v[1] * Math.cos(angle) ]; } function distance(point_A, point_B) { return Math.sqrt( square(point_A[0] - point_B[0]) + square(point_A[1] - point_B[1])); }
Next, we define functions for creating simple geometric primitives: points, lists of points, rays, lines, segments, circles, and circular arcs. These are represented as simple Javascript objects (hashmaps).
function create_pointlist_array(pts) { var args = pts.slice(0); for(var i=0; i<args.length;i++) { if(args[i].shape == "pointlist") { var edit = [i, 1]; edit = edit.concat(args[i].points); Array.prototype.splice.apply(args, edit); i--; } } // singleton lists become bare points, etc. //console.log("pointlist array[] args",args,args.length, distinct(args)); if(args.length == 0){return null;} if(args.length == 1){return args[0];} return { "shape": "pointlist", "points": distinct(args) }; } function create_pointlist() { var args = []; for(var i=0; i<arguments.length;i++) { args.push(arguments[i]); } for(var i=0; i<args.length;i++) { if(args[i].shape == "pointlist") { var edit = [i, 1]; edit = edit.concat(args[i].points); Array.prototype.splice.apply(args, edit); i--; } } // singleton lists become bare points, etc. //console.log("pointlist args",args,args.length, distinct(args)); if(args.length == 0){return null;} if(args.length == 1){return args[0];} return { "shape": "pointlist", "points": distinct(args) }; } function create_point(P) { return {"shape":"point", "x":P[0], "y":P[1]};} function create_circle(x,y,r) { return {"shape" : "circle", "center_x": x, "center_y": y, "radius": r}; } function create_line(x,y,dx,dy) { return {"shape" : "line", "x": x, "y":y, "dx":dx, "dy": dy}; } function create_segment(x1,y1,x2,y2) { return {"shape":"segment", x1 : x1, y1 : y1, x2 : x2, y2 : y2}; } function create_ray(x,y,dx,dy) { return {"shape":"ray", x: x, y: y, dx: dx, dy: dy}; } function create_arc(x1, y1, x2, y2, curvature) { return {"x1":x1, "y1":y1, "x2":x2, "y2":y2, "curvature":curvature, "shape":"arc"}; } function points(x) { // Takes either a pointlist or a point and returns a list of points return x.shape == "pointlist" ? x.points : [x]; }
To convert partial figures (rays and circular arcs) into their fully extended counterparts (lines and circles), we provide the following functions.
function ray_to_line(ray) {return $.extend(true,{}, ray, {"shape":"line"});} function arc_to_circle(arc) { // Find the center of the circle: locate the perpendicular // bisector of the two arc points; scale and flip it so that it's // a unit vector pointing towards the center of the circle; // multiply by the distance from the midpoint to the circle's // center and add the resulting vector to the midpoint. var r = 1/arc.curvature; var bis = perpendicular_bisector([arc.x1, arc.y1], [arc.x2, arc.y2]); var centripetal = vector_scale(sign(r), normalize([bis.dx, bis.dy])); var d = distance([arc.x2, arc.y2],[arc.x1, arc.y1]); var h = Math.sqrt(r*r - d*d/4) || 0; // accounts for small errors var center = vector_add([bis.x, bis.y], vector_scale(h, centripetal)); return create_circle(center[0], center[1], Math.abs(r)); }
6.4 Geometric intersections
The function figure-intersection takes any two of the primitive
geometric figures defined in the previous section and returns a figure
representing the places where they overlap (or null, if the two shapes
don't overlap at all.) For example, the intersection of two lines may
be a single point, a line, or null.
The function dispatches on the type of object involved, calling a
specialized subprocedure such as figure_intersection_line_circle.
function figure_intersection(fig1, fig2) { if(!fig1 || !fig2){return null;} var sig = [fig1["shape"], fig2["shape"]]; var match = function(x){return equal_arrays(sig, x);} if(match(["line", "circle"])){ return figure_intersection_line_circle(fig1, fig2); } else if( match(["circle", "line"])) { return figure_intersection_line_circle(fig2, fig1); } else if( match(["circle", "line"])) { return figure_intersection_line_circle(fig2, fig1); } else if( match(["point", "point"])) { return figure_intersection_point_point(fig1, fig2); } else if( match(["ray", "ray"])) { return figure_intersection_ray_ray(fig1, fig2); } else if( match(["circle", "ray"])) { return figure_intersection_ray_circle(fig2, fig1); } else if( match(["ray","circle"])) { return figure_intersection_ray_circle(fig1, fig2); } else if( match(["arc", "ray"])) { return figure_intersection_ray_arc(fig2, fig1); } else if( match(["ray","arc"])) { return figure_intersection_ray_arc(fig1, fig2); } else if( match(["ray","point"])) { return figure_intersection_ray_point(fig1, fig2); } else if( match(["point","ray"])) { return figure_intersection_ray_point(fig2, fig1); } else if( match(["ray","segment"])) { return figure_intersection_ray_segment(fig1, fig2); } else if( match(["segment","ray"])) { return figure_intersection_ray_segment(fig2, fig1); } } function figure_intersection_ray_point(ray, pt) { var q_p = vector_subtract([pt.x, pt.y], [ray.x, ray.y]); var dr = [ray.dx, ray.dy]; if(// collinear approximately(0, determinant(q_p, dr)) && dot_product([ray.dx, ray.dy], vector_subtract([pt.x, pt.y], [ray.x, ray.y])) >= 0) { return pt; } return null; } function figure_intersection_ray_segment(ray, seg) { var p = create_ray(seg.x1, seg.y1, seg.x2 - seg.x1, seg.y2 - seg.y1); var q = create_ray(seg.x2, seg.y2, seg.x1 - seg.x2, seg.y1 - seg.y2); //console.log("rayseg",ray,p,figure_intersection(ray,p)); // var $svg = $("svg").last().svg().svg("get"); // var u = vector_scale(0.3, normalize([ray.dx, ray.dy])); // $svg.line(to_page($svg,[ray.x, ray.y])[0], // to_page($svg,[ray.x, ray.y])[1], // to_page($svg,[ray.x + u[0], ray.y + u[1]])[0], // to_page($svg,[ray.x + u[0], ray.y + u[1]])[1], // {"stroke":"#f00"}); // var u = vector_scale(0.3, normalize([p.dx, p.dy])); // $svg.line(to_page($svg,[p.x, p.y])[0], // to_page($svg,[p.x, p.y])[1], // to_page($svg,[p.x + u[0], p.y + u[1]])[0], // to_page($svg,[p.x + u[0], p.y + u[1]])[1], // {"stroke":"#00f"}); // console.log(to_page($svg,[ray.x, ray.y])); // console.log(to_page($svg,[ray.x + u[0], ray.y + u[1]])); return figure_intersection( figure_intersection(ray, p), figure_intersection(ray, q)); } function figure_intersection_point_point(pt1, pt2){ if(approximately(pt1.x, pt2.x) && approximately(pt1.y, pt2.y)){ return pt1; } return null; } function figure_intersection_ray_ray(ray1, ray2){ // First, determine the intersection of the corresponding lines. // Then restrict to the positive side of both rays. var v1 = [ray1.dx, ray1.dy]; var v2 = [ray2.dx, ray2.dy]; var det = determinant(v1, v2); //console.log("ray ray ::", ray1, ray2, det); //var $svg = debug_svg(); // debug if(det != 0) { // Single point where the corresponding lines intersect var q_p = vector_subtract([ray2.x, ray2.y], [ray1.x, ray1.y]); var t = ray2.dy*(ray2.x - ray1.x) - ray2.dx*(ray2.y - ray1.y); t = t/det; var meet = create_point(vector_add([ray1.x, ray1.y], vector_scale(t, [ray1.dx, ray1.dy]))); //dot([meet.x, meet.y]).draw($svg); // debug if(figure_intersection(meet, ray1) && figure_intersection(meet, ray2)) { return meet; } return null; } var a = figure_intersection(create_point([ray2.x, ray2.y]), ray1); var b = figure_intersection(create_point([ray1.x, ray1.y]), ray2); if(!a && !b) { // either <--• •-->, or the lines never meet. return null; } else if(a && b) { // •--> <--• return create_segment(ray1.x, ray1.y, ray2.x, ray2.y); } // •--> •--> return a ? ray2 : ray1; } function figure_intersection_line_circle(line, circle){ // quadratic solution var p = [line.x, line.y]; var q = [circle.center_x, circle.center_y]; var v = [line.dx, line.dy]; var r = circle.radius; var p_q = vector_subtract(p,q); var A = dot_product(v,v); var B = dot_product(p_q, v); // /half/ the linear term, actually. var C = dot_product(p_q, p_q)-r*r var discriminant = B*B - A*C; var t0 = -B/A; //console.log(discriminant); if(discriminant == 0) { return create_point(vector_add(p, vector_scale(t0, v))); } else if (discriminant > 0) { var t1 = t0 + Math.sqrt(B*B - A*C)/A; var t2 = t0 - Math.sqrt(B*B - A*C)/A; return create_pointlist( create_point(vector_add(vector_scale(t1, v), p)), create_point(vector_add(vector_scale(t2, v), p))); } return null; } function figure_intersection_ray_circle(ray, circle){ // console.log("figure intersection ray circle ::"); var overlap = figure_intersection_line_circle(ray_to_line(ray), circle); if(!overlap) {return null;} var pts = points(overlap); // Find the points where the ray-as-line meets the circle, and // select only those that lie in the positive direction of the // ray. pts = filter(function(pt){ return dot_product( [ray.dx, ray.dy], vector_subtract( [pt.x, pt.y], [ray.x, ray.y])) >= 0; }, pts); return create_pointlist_array(pts); } function figure_intersection_ray_arc(ray, arc, debug){ if(debug){ var svg = svg_diagram(1,create_diagram()).appendTo($workspace); var $svg = $(svg).svg().svg("get"); var x = connected_figure().add_point("A", [arc.x1, arc.y1]).add_point( "B",[arc.x2, arc.y2]).add_connection("A","B",[arc.curvature]); x.draw($svg); dot([ray.x, ray.y]).draw($svg, {"fill":"#a00"}); var xy = to_page($svg, [ray.x, ray.y]); var pq = vector_add(xy, vector_scale(128, [ray.dx, -ray.dy])); $svg.line(xy[0], xy[1], pq[0],pq[1], {"stroke":"#00a"} ); debug[0].draw($svg,{"stroke":"#fcc","strokeWidth":0.5}); debug[1].draw($svg,{"stroke":"#ccc"}); } if(approximately(0, arc.curvature)){ var overlap = figure_intersection(ray, create_segment(arc.x1, arc.y1, arc.x2, arc.y2)); if(debug && overlap) { dot([overlap.x, overlap.y]).draw($svg); $(svg).css("background","#fffff0"); } return overlap; } var overlap = figure_intersection_ray_circle(ray, arc_to_circle(arc)); if(!overlap){return null;} var pts = points(overlap); var bis = vector_subtract([arc.x2, arc.y2], [arc.x1, arc.y1]); bis = vector_scale(-sign(arc.curvature), [bis[1], -bis[0]]); var mid = midpoint([arc.x1, arc.y1], [arc.x2, arc.y2]); // Keep only those points that are on the "positive" side of the // line joining the two arc endpoints. var pts = points(overlap); if(debug) { var pts2 = pts.filter(function(pt) { return dot_product(bis, vector_subtract([pt.x, pt.y], mid)) <= 0; }); for(var i in pts2) { var pt = pts2[i]; var xy = [pt.x,pt.y]; dot(xy).draw($svg); $(svg).css("background","#fee"); } } return create_pointlist_array(pts.filter(function(pt) { return dot_product(bis, vector_subtract([pt.x, pt.y], mid)) <= 0; })); }
6.5 Pieces of lines and circles
Circular arcs and line segments are the building blocks of the figures used in the ANALOGY program.
function arc_length(point_A, curvature, point_B) { var d = distance(point_A, point_B); if(curvature == 0){return d;} return 2/curvature*Math.asin( d*curvature/2 ); } function arc_centroid(point_A, curvature, point_B) { // return the centroid of the given arc // (signed curvature indicates direction, by convention) var midpoint = vector_scale(0.5, vector_add(point_A, point_B)); if(curvature == 0) { return midpoint; } var d = distance(point_A, point_B); var angle = Math.asin(d*curvature/2); // HALF the angle contained between point_A and point _B (& center of arc's circle) // Given a circular segment centered at the origin // and oriented symmetrically about the y-axis, its // x-center is 0 and its y-center is as follows: var y_center = 4*Math.pow(Math.sin(angle),3)/(3*curvature*(2*angle - Math.sin(2*angle))); // Translate to get the distance from the midpoint to the // centroid. y_center = Math.abs(y_center) - sign(curvature)*Math.cos(angle)/curvature; // Get a vector pointing from the midpoint to the tip of the arc. var perp = (function(x) { return vector_scale(sign(curvature), [x[1], -x[0]]); })(vector_subtract(point_B, point_A)); if(curvature < 0) { // console.log("norm perp",normalize(perp)); // console.log("y_center",y_center); // console.log("midpoint",midpoint); // console.log("scaled perp",vector_scale(y_center, normalize(perp))); // console.log("final",vector_add(midpoint, vector_scale(y_center, normalize(perp)))); } // Scale the vector accordingly, and add it to the midpoint to get the final result. return vector_add(midpoint, vector_scale(y_center, normalize(perp))); } function centroid(fig) { // Compute the geometric center of the figure if(fig.type == "DOT") { return fig.position; } else if(fig.type == "SCC") { var centroid = [0,0]; var total_arc_length = 0; for(var i=0; i<fig.junction.length-1; i+=2) { var a = fig.junction[i+0]; var b = fig.junction[i+1]; var c = fig.junction[i+2]; var ds = arc_length(a,b,c); total_arc_length += ds; centroid = vector_add(centroid, vector_scale(ds, arc_centroid(a,b,c))); } return vector_scale(1/total_arc_length, centroid); var pts = fig.points(); return vector_scale(1/pts.length, pts.reduce(vector_add)); } else { var pts = []; for(var x in fig.coordinates){pts.push(fig.coordinates[x]);} var curves = fig.curves(); for(var i in curves) { for(var j=2;j<curves[i].length-2;j+=2) { pts.push(curves[i][j]); } } pts = distinct(pts); return vector_scale(1/pts.length, pts.reduce(vector_add)); } } function center(fig) { // Approximate the geometric center of the figure using the center // of mass of its junctions. if(fig.type == "DOT") { return fig.position; } else if(fig.type == "SCC") { var pts = fig.points(); return vector_scale(1/pts.length, pts.reduce(vector_add)); } else { var pts = []; for(var x in fig.coordinates){pts.push(fig.coordinates[x]);} var curves = fig.curves(); for(var i in curves) { for(var j=2;j<curves[i].length-2;j+=2) { pts.push(curves[i][j]); } } pts = distinct(pts); return vector_scale(1/pts.length, pts.reduce(vector_add)); } }
6.6 Primitive drawing functions
The following functions perform low-level drawing capabilities using SVG graphics.
var pen_style = { fill:'none', stroke: '#444444', strokeWidth:1.6, }; function svg_new(width, height) { var svg = document.createElementNS("http://www.w3.org/2000/svg", "svg"); svg.setAttribute('width', width); svg.setAttribute('height', height); svg.setAttributeNS("http://www.w3.org/2000/xmlns/", "xmlns:xlink", "http://www.w3.org/1999/xlink"); return svg; } function to_page($svg, xy) { // Convert Evans's unit square coordinates to svg coordinates. var w = ww; var w = $svg._svg.attributes[0].value; var h = w; if(typeof xy == "number"){ return xy * w; } else { return [xy[0] * w, (1-xy[1]) * h]; } } function draw_arc($svg, start, curve, end, attrs) { var attrs = $.extend({},pen_style,attrs); var start = to_page($svg, start); var end = to_page($svg, end); var path = $svg.createPath(); path.move(start[0],start[1]); if(curve == 0) { path.line(end[0],end[1]); } else { var radius = to_page($svg, Math.abs(1/curve)); path.arc( radius, radius, 0, false, !(curve > 0), end[0], end[1]); } $svg.path(path,attrs); }
Footnotes:
Connections are symmetric, so connecting "A" and "B" creates a symmetric connection between "B" and "A"; you don't have to worry about the order of the arguments.
Because Javascript uses a call-by-object-sharing paradigm, it's sometimes useful to clone a map so that you can modify the copy without affecting the original.